Full view of the ground with the San Andreas fault running through the middle of the image. A 30 foot steam offset from the 1857 earthquake can be seen near the right edge of the image.
Can the position of the moon or the planets affect seismicity? Are there more earthquakes in the morning/in the evening/at a certain time of the month?
Earthquakes are equally as likely to occur in the morning or the evening. Many studies in the past have shown no significant correlations between the rate of earthquake occurrence and the semi-diurnal tides when using large earthquake catalogs.
Several recent studies, however, have found a correlation between earth tides (caused by the position of the moon relative to the earth) and some types of earthquakes. One study, for example, concludes that during times of higher earth and ocean tides, such as during times of full or new moon, earthquakes are more likely on shallow thrust faults near the edges of continents and in (underwater) subduction zones. Lunar or solar eclipses represent, of course, special cases of full and new moon, but do not cause any special or different tidal effects from full and new moon.
Earth tides (Earth's surface going up and down by a couple of centimeters) and especially ocean tides (surface of the ocean going up and down by a meter or more) raise and lower the confining pressure on shallow, dipping faults near continental edges and in subduction zones.
When the confining pressure is lessened, the faults are unclamped and more likely to slip. The increased probability is a factor of ~3 during high tides. But you must stop and realize that the background probability is, in general, very low in a given place and year (fractions of a percent), so that raising this tiny probability by a factor of 3 during high tides still results in a very tiny probability.
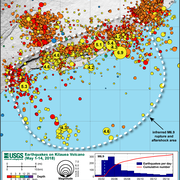
There have also been some small but significant correlations reported between the semi-diurnal tides and the rate of occurrence of aftershocks in some volcanic regions, such as Mammoth Lakes.
The moon, sun, and other planets have an influence on the earth in the form of perturbations (small changes) to the gravitational field. The relative amount of influence is proportional to the objects mass, and inversely proportional to the third power of its distance from the earth.
The stresses induced in the earth by an extraterrestrial mass are proportional to the gravitational field gradient dg( r ) / dr and NOT to the gravitational field g( r ). g( r ) = GMm / r^2 thus: dg( r ) / dr = -2 * g( r ) / r = -2GMm / r^3
Related
What is an earthquake and what causes them to happen?
An earthquake is caused by a sudden slip on a fault. The tectonic plates are always slowly moving, but they get stuck at their edges due to friction. When the stress on the edge overcomes the friction, there is an earthquake that releases energy in waves that travel through the earth's crust and cause the shaking that we feel. In California there are two plates - the Pacific Plate and the North...
Foreshocks, aftershocks - what's the difference?
"Foreshock" and "aftershock" are relative terms. Foreshocks are earthquakes that precede larger earthquakes in the same location. An earthquake cannot be identified as a foreshock until after a larger earthquake in the same area occurs. Aftershocks are smaller earthquakes that occur in the same general area during the days to years following a larger event or "mainshock." They occur within 1-2...
What is surface faulting or surface rupture in an earthquake?
Surface rupture occurs when movement on a fault deep within the earth breaks through to the surface. NOT ALL earthquakes result in surface rupture.
At what depth do earthquakes occur? What is the significance of the depth?
Earthquakes occur in the crust or upper mantle, which ranges from the earth's surface to about 800 kilometers deep (about 500 miles). The strength of shaking from an earthquake diminishes with increasing distance from the earthquake's source, so the strength of shaking at the surface from an earthquake that occurs at 500 km deep is considerably less than if the same earthquake had occurred at 20...
Why are there so many earthquakes in the Geysers area in Northern California?
The Geysers Geothermal Field is located in a tectonically active region of Northern California. The major seismic hazards in the region are from large earthquakes occurring along regional faults that are located miles away from the geothermal field, such as the San Andreas and Healdsburg-Rodgers Creek faults. However, activities associated with the withdrawal of steam for producing electric power...
Do earthquakes occur in Antarctica?
Earthquakes do occur in Antarctica, but not very often. There have been some big earthquakes--including one magnitude 8.1 --in the Balleny Islands (between Antarctica and New Zealand). The boundary between the Scotia Plate and the Antarctic Plate just grazes the north tip of the Antarctic Peninsula (look "northwest" from the Pole toward South America). There is also a hint of a line of seismicity...
Can we cause earthquakes? Is there any way to prevent earthquakes?
Earthquakes induced by human activity have been documented at many locations in the United States and in many other countries around the world. Earthquakes can be induced by a wide range of causes including impoundment of reservoirs, surface and underground mining, withdrawal of fluids and gas from the subsurface, and injection of fluids into underground formations. While most induced earthquakes...
What is the difference between aftershocks and swarms?
Aftershocks are a sequence of earthquakes that happen after a larger mainshock on a fault. Aftershocks occur near the fault zone where the mainshock rupture occurred and are part of the "readjustment process” after the main slip on the fault. Aftershocks become less frequent with time, although they can continue for days, weeks, months, or even years for a very large mainshock. A swarm, on the...
Full View of the San Andreas Fault
Full view of the ground with the San Andreas fault running through the middle of the image. A 30 foot steam offset from the 1857 earthquake can be seen near the right edge of the image.
Related
What is an earthquake and what causes them to happen?
An earthquake is caused by a sudden slip on a fault. The tectonic plates are always slowly moving, but they get stuck at their edges due to friction. When the stress on the edge overcomes the friction, there is an earthquake that releases energy in waves that travel through the earth's crust and cause the shaking that we feel. In California there are two plates - the Pacific Plate and the North...
Foreshocks, aftershocks - what's the difference?
"Foreshock" and "aftershock" are relative terms. Foreshocks are earthquakes that precede larger earthquakes in the same location. An earthquake cannot be identified as a foreshock until after a larger earthquake in the same area occurs. Aftershocks are smaller earthquakes that occur in the same general area during the days to years following a larger event or "mainshock." They occur within 1-2...
What is surface faulting or surface rupture in an earthquake?
Surface rupture occurs when movement on a fault deep within the earth breaks through to the surface. NOT ALL earthquakes result in surface rupture.
At what depth do earthquakes occur? What is the significance of the depth?
Earthquakes occur in the crust or upper mantle, which ranges from the earth's surface to about 800 kilometers deep (about 500 miles). The strength of shaking from an earthquake diminishes with increasing distance from the earthquake's source, so the strength of shaking at the surface from an earthquake that occurs at 500 km deep is considerably less than if the same earthquake had occurred at 20...
Why are there so many earthquakes in the Geysers area in Northern California?
The Geysers Geothermal Field is located in a tectonically active region of Northern California. The major seismic hazards in the region are from large earthquakes occurring along regional faults that are located miles away from the geothermal field, such as the San Andreas and Healdsburg-Rodgers Creek faults. However, activities associated with the withdrawal of steam for producing electric power...
Do earthquakes occur in Antarctica?
Earthquakes do occur in Antarctica, but not very often. There have been some big earthquakes--including one magnitude 8.1 --in the Balleny Islands (between Antarctica and New Zealand). The boundary between the Scotia Plate and the Antarctic Plate just grazes the north tip of the Antarctic Peninsula (look "northwest" from the Pole toward South America). There is also a hint of a line of seismicity...
Can we cause earthquakes? Is there any way to prevent earthquakes?
Earthquakes induced by human activity have been documented at many locations in the United States and in many other countries around the world. Earthquakes can be induced by a wide range of causes including impoundment of reservoirs, surface and underground mining, withdrawal of fluids and gas from the subsurface, and injection of fluids into underground formations. While most induced earthquakes...
What is the difference between aftershocks and swarms?
Aftershocks are a sequence of earthquakes that happen after a larger mainshock on a fault. Aftershocks occur near the fault zone where the mainshock rupture occurred and are part of the "readjustment process” after the main slip on the fault. Aftershocks become less frequent with time, although they can continue for days, weeks, months, or even years for a very large mainshock. A swarm, on the...
Full View of the San Andreas Fault
Full view of the ground with the San Andreas fault running through the middle of the image. A 30 foot steam offset from the 1857 earthquake can be seen near the right edge of the image.
Full view of the ground with the San Andreas fault running through the middle of the image. A 30 foot steam offset from the 1857 earthquake can be seen near the right edge of the image.